What is polygon?

In elementary geometry, a polygon (/ˈpɒlɪɡɒn/) is a plane) figure that is bounded by a finite chain of straight line segments closing in a loop to form a closed polygonal chain or circuit. (cited from wikipedia )

近况

最近一直在学习多边形图形处理方面的知识，非科班出身的我接触到这些知识，首先就是惊叹为什么这些方法这么神奇，同时也充满着迷茫，懵懵懂懂！今天借着除草之际，特将关于多边形图形处理方面的内容记录于此。为啥我要学习这方面的内容呢？与我当前学习的数值算法有关，当解决一个多边形区域内的偏微分方程时，将区域均匀地离散成许多点，对求解精度具有一定的影响。所以，寻找一种理想的离散多边形区域的算法至关重要。前段时间，找到了一篇关于采用区域内点距边界距离函数均匀mesh区域的Paper，受益匪浅，也想亲自写一写来体会其中的奥秘owo。这其中，遇到了几个问题。

如何判断一点在边界内、边界外、边界上？

在网路上搜索这类算法，有很多，但是，很多并不完备。我觉得很不错的方法是射线法，这让我觉得好神奇，数学的奥妙！如下说：

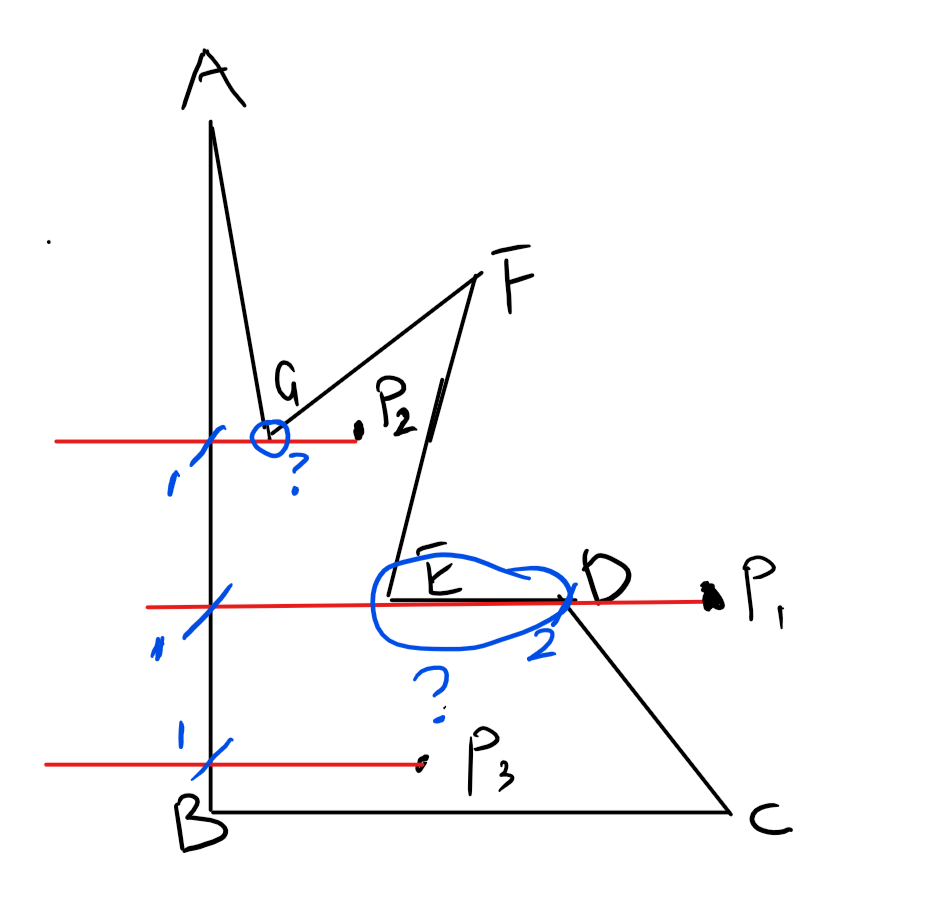
这里的多边形由A、B、C、D、E、F、G 7个顶点围成，其中P1,P2,P3分别为三个判断点。

射线法的基本步骤是，在判断点处作一条水平或者的竖直的射线，如果射线与图形相交的点数为奇数，则点在图形内部，反之则在图形外部。

算法的实施基本是遍历每一条边与点或射线的关系。

这里主要要考虑两种特殊情况，如点P1和P2所示，第一种情况，射线与多边形一条边共线，这里采用的办法是直接不考虑这条边，无视它与射线共线。第二种情况，两条边的交点在射线上，这里处理方法是判断这个交点的纵坐标是否是边端点较大的点，是则记这点为射线与图形的交点，否则忽视。

具体的Matlab实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

function s = pointInPolygon(p, pv)
% pv为多边形的个顶点，这里要求为[x,y],p为判断点
% 判断点是否在多边形内部，是返回1，否返回-1，在边界上返回0
n = length(pv(:,1));
count = 0;
s = 2;
for i = 1:n-1
    if abs((pv(i,1)-p(1)).*(pv(i+1,2)-p(2))-(pv(i+1,1)-p(1)).*(pv(i,2)-p(2))) <= eps && ...
            min(pv(i:i+1,1)) <= p(1) && p(1) <= max(pv(i:i+1,1)) && ...
            min(pv(i:i+1,2)) <= p(2) && p(2) <= max(pv(i:i+1,2))   % p点在边上
        s = 0;
        break
    elseif pv(i,2) ~= pv(i+1,2) && max(pv(i:i+1,1)) <= p(1)     % 边s非水平且在射线一侧
        if any(max(pv(i:i+1,2))==p(2))                         % 边的端点（纵坐标较大的点）在射线上
            count = count + 1;
        elseif min(pv(i:i+1,2)) < p(2) && p(2) < max(pv(i:i+1,2)) % 边与射线相交
            count = count + 1;
        end
    end
end

if mod(count,2)==1 && s ~= 0
    s = 1;
elseif s ~= 0
    s = -1;
end

end

如何求得点到多边形边界的距离

这里比较简单了，计算点到每条边的距离，取最小值。但是，要考虑垂足是否落在边上。这里不赘述，实现的Matlab代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

function d = pointToSegmentDist(p, a, b)
% a,b,p均为一点的坐标
ab = b - a;
ap = p - a;
t = sum(ab.*ap, 2)/sum(ab.*ab, 2);
if t < 0
    d = norm(ap);
elseif t > 1
    bp = p - b;
    d = norm(bp);
else
    ad = t * ab;
    d = norm(ad - ap);
end
end

Be a Cyberslacker

日常摸鱼的我，终于学到了一个准确描述摸鱼的单字owo——cyberslack。生生不息，摸鱼不止，已成为摸鱼党的工作信条了。回想过往的半个月，混混沌沌，挖了各种坑，但是不填！无奈，只好将摸鱼之时学到的知识搬到这里来充实一下自己因摸鱼无比空虚的内心owo。抬头一看，又忽然发觉那本还没看完的《撒哈拉的故事》，OTZ，再次立一个flag，下一篇拔草文之前看完owo。最近被老师感染着快要有创业的想法了，只是，总感觉自己要学的内容实在太多了，如果留下来继续的话，会很不安心的owo。如果我学会了优雅地摸鱼，也许我会留下吧。

Ummm，前些天玩了慢慢罪恶感的Undertale，已经到了最后的关卡了，但是感觉自己已经过不去了qwq，膜拜大神。

Ummm，昨天是万圣节，看见了竹萌里好多大佬的房子，献上我的膝盖owo，当然，最惬意的还是Trick or treat，真的敲开心owo！

Ummm，今天是凛喵的生日，很可惜，全部保底，明天集齐50♥看自己是不是非酋。

Ummm，拔草怎么越拔越不想睡觉呢？但是我已经写不下去了，词穷，滚去睡了~~~~

Oyasumi! The whole world.