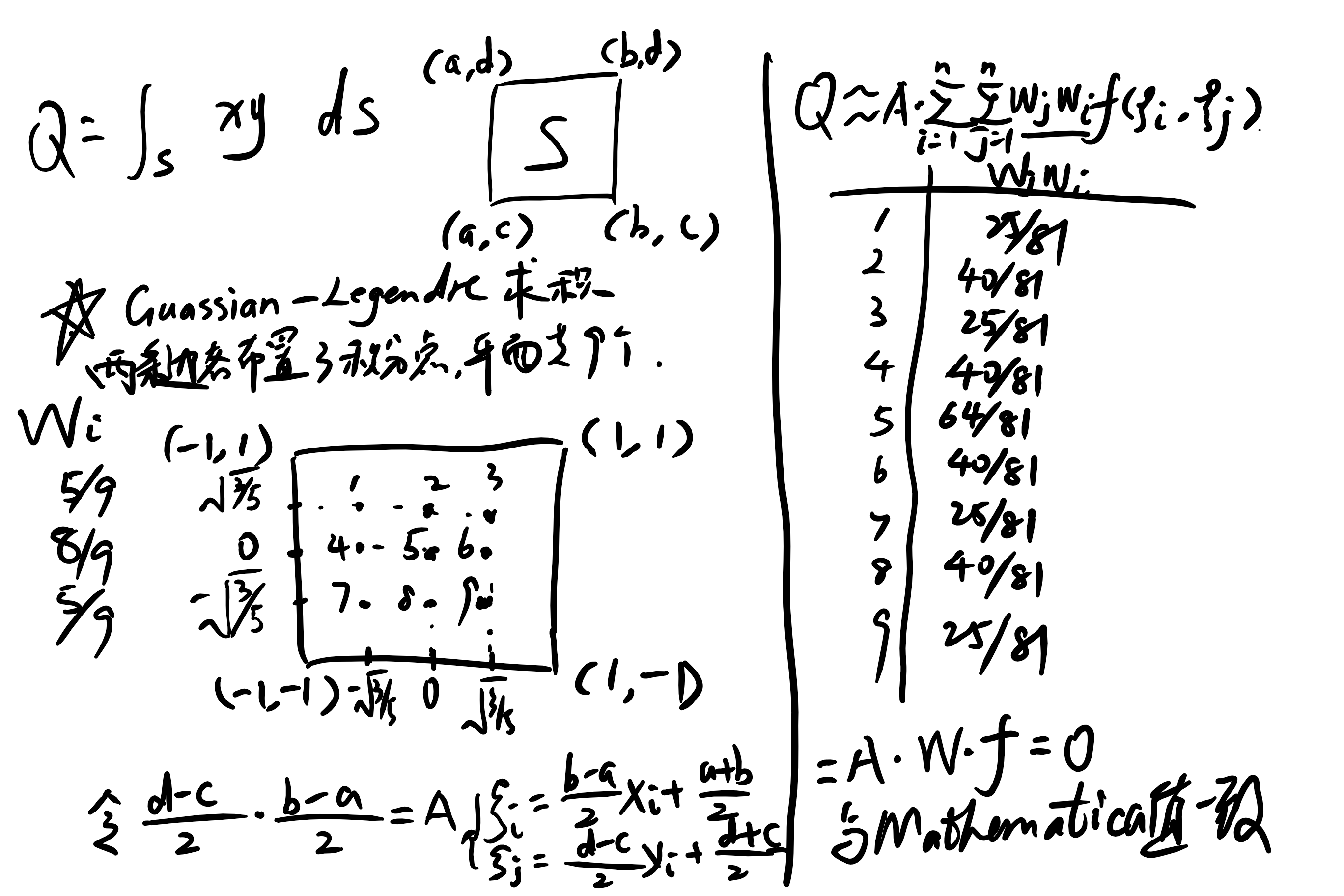高斯数值积分这棵草养了很久了，一直想拔掉，苦于可怕的拖延症。今天趁着礼拜六的闲暇之际，将Guassian-Legendre 求积用Python实现了一遍，为以后的MLPG算法编写填点土owo。

以下为高斯-勒让得 求积得演算过程

1

得到的结果与Mathematicia结果一致。这里积分域为-1<=x<=1 & -1<=y<=1。

以下为Python实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import numpy as np


class Integrate(object):

    def __init__(self):
        self.x = np.array([2, 4])   # x的积分域
        self.y = np.array([1, 2])   # y的积分域
        self.w_g = np.array([25/81, 40/81, 25/81, 40/81, 64/81, 40/81, 25/81, 40/81, 25/81])
        # 高斯点权值这里采用三点积分
        a = np.sqrt(3/5)
        self.g_x = np.array([-a, 0, a, -a, 0, a, -a, 0, a])
        self.g_y = np.array([a, a, a, 0, 0, 0, -a, -a, -a])
        self.xi = np.array([])
        self.yi = np.array([])
        self.ans = 0

    def cor(self):
        self.xi = (self.x[1]-self.x[0])/2*self.g_x+(self.x[0]+self.x[1])/2
        self.yi = (self.y[1]-self.y[0])/2*self.g_y+(self.y[1]+self.y[0])/2

    def integrate(self):
        self.ans = (self.x[1]-self.x[0])/2*(self.y[1]-self.y[0])/2*self.w_g.dot(self.xi*self.yi)         # f=xy

数值积分的形式有许多种，这里仅采用Guassian-Legendre 求积作为示例。